KMP算法 —— 字符串匹配

KMP算法 —— 字符串匹配

五月 13, 2020

KMP算法 —— 字符串匹配

设有两个字符串s1,s2

一般写法

从左往右依次对比s1[i]与s2[j]是否匹配，如果不匹配，就跳回i = 1处（向右移1位），重新进行匹配。

简单来说就是一位一位匹配是否相同。

时间复杂度：O（n*m)

第一次优化 普通KMP（无next计算优化）

因为不匹配的时候，前面除了这个字符，前面的字符一定全部匹配，将i移回i = 1处一定不匹配。

所以我们得出：i可以不改变，只改变模式串s2的位置就可以了。

**怎么改变s2的位置？**这是KMP算法的核心。

我们手动模拟一下：

此时C和D不匹配，显然，我们要将j移动到 j = 1处，为什么？因为显然前面有一个**'A'与s2[0]**相同

类似的

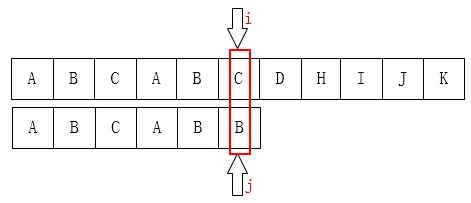
可以把j移动到j = 2的位置，因为s2[0] == 'A' && s2[1] == 'B'

在模拟中，我们可以大致看出，当匹配失败时，j要移动的下一个位置k，有这样的性质：最前面的k个字符和j之前的最后k个字符是相同的。

即

S2[0,k−1]=S2[j−k,j−1]S2[0,k-1] = S2[j-k,j-1]

举个例子：

为什么可以直接将j移动到k而不比较前面k个字符？

  • 推导如下:

    ​ 当**S1[i] != S2[j]**时，

    ​ 有 S1[i-j , i-1] == S2[0 , j-1]

    ​ 又因S2[0 , k-1] == S2[j-k , j-1]

    ​ 所以有 S1[i-k , i-1] == S2[0 , k-1]

现在问题转化到，我们怎么求这个（些）k？

因为每一个位置都有可能发生不匹配，所以我们对s2的每一个位置都要求出一个k值，我们就用数组next[]来表示——s2的第j位不匹配时(s1[i] != s2[j])，j指针的下一个位置，即next[j] = k

这个next[j]的含义也可以这样表示——S2[0 , next[j]-1] == S2[j-next[j] , j-1],即next[j] = k

S2 A B C D A B D
j 0 1 2 3 4 5 6
next -1 0 0 0 0 1 2

从表格里看出，我们初始化next[0] = -1，为什么？

当j = 0时，j已经在最左边，不能移动了，这时候应该将i指针后移一位。所以才有next[0] = -1这样的初始化，对next[j]特殊判断，如果next[j] == -1，说明此时j在s2的最左边，要将i指针后移一位。

S2 A B C A B C D
j 0 1 2 3 4 5 6
next -1 0 0 0 1 2 3

仔细观察，我们可以看出：

当S2[next[j]] == S2[j]时 (S2[k] == S2[j]) // S[2] == S[5]

有next[j+1] == next[j] + 1 // next[6] == next[5] + 1

即，当前s2[j]位于一个与前面某个子字符串相同的子字符串里。'ABC' == 'ABC'

可以证明，如下：

​ 因为S2[0 , k-1] == S2[j-k , j-1] (next[j] == k)

​ 当S2[k] == S2[j]，

​ 我们可以得到：S2[0 , k-1] + S2[k] == S2[j-k , j-1] + S2[j]

​ 即：S2[0 , k] == S2[j-k , j]，

​ 即，向后移一位仍满足**S2[0 , k-1] == S2[j-k , j-1]**的形式，且长度+1

​ 即next[j+1] == k+1 == next[j] + 1

那如果**S2[next[j]] != S2[j]**呢 (S2[k] != S2[j])

S2 A B A C D A B A B C
j 0 1 2 3 4 5 6 7 8 9
next -1 0 0 1 0 0 1 2 3 2

我们把**S2[0 , k]和S2[j-k ~ ]**拿出来

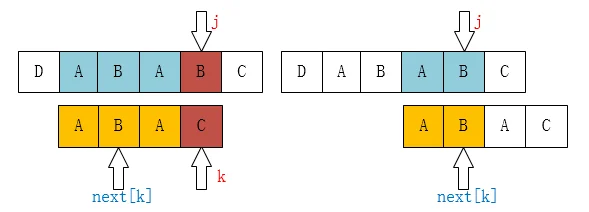
显然，我们可以得出此时k = next[k]

因为我们此时已经找不到"ABAB"这样的后缀子串了，但是我们还可能找到“AB”、“B”这样的前缀子串。为了效率，我们要找尽量长的子串"AB"即：当前k的上一个k值，或者说是找k的k。

因为我们每次都取尽量长的子串，即当前位置最优解，如果这个位置不符合就找这个位置不符合时所对应的上个位置（即k的k），而k的k如果不符合，我们继续找k的k的k······

我们可以看出 k = next[k] 相当于一个递归调用。

这样我们怎么获得k的问题就解决了，可以写出以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int* getNext(string s2)
{
    int* next = (int*)calloc(s2.length(),sizeof(int));
    next[0] = -1;
    int k = -1;
    int j = 0;
    while(j < s2.length())
    {
        if (k == -1 || s2[j] == s2[k])
        {
            next[++j] = ++k;
        }
        else
        {
            k = next[k];
        }
    }
    return next;
}

第二次优化 next计算的优化

观察下面的例子：

依据我们上面的算法，得到的next数组应该是[-1, 0, 0, 1]

所以我们下一步把j移动到1位置：

不难发现，这一步完全木得意义，因为后面的B已经不匹配了，前面的B也一定不匹配，同样的情况也发生在第二个A上。

显然，问题发生的原因在于：S2[j] == S2[next[j]]。

所以，对于这个问题的优化，我们只需要添加一个判断条件即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int* getNext(string s2)
{
    int* next = (int*)calloc(s2.length(),sizeof(int));
    next[0] = -1;
    int k = -1;
    int j = 0;
    while(j < s2.length())
    {
        if (k == -1 || s2[j] == s2[k])
        {
        	if(s2[++j] == s2[++k])
            	next[j] = next[k];		//这一步与k = next[k]一个原理
            else
            	next[j] = k;
        }
        else
        {
            k = next[k];
        }
    }
    return next;
}

代码们

KMP的核心就在于求next数组，解决了这个问题，这个程序就很容易写出来了。

主要函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int KMP(string s1,string s2)		//这个用来找s2在s1中第一次出现的位置，如果在s1中找不到s2返回-1
{
    int i = 0,j = 0;	//s1[i],s2[j]
    int* next = getNext(s2);
    while(i < s1.length() && j < s2.length())
    {
        if(j == -1 || s1[i] == s2[j])		//当j==-1时，要移动的是i，当然j也要+1变成0
        {
            i++;
            j++;
        }
        else
        {
            j = next[j];
        }
    }
    if(j == s2.length())
    {
        return i - j;
    }
    else
    {
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void KMP(string s1,string s2) //这个用于求s2在s1中出现的所有位置
{
    int i = 0,j = 0;
    queue<int> q;
    int* next = getNext(s2);
    while(i < s1.length())
    {
        if(j == -1 || s1[i] == s2[j])
        {
            i++;
            j++;
        }
        else
        {
            j = next[j];
        }

        if(j == s2.length())
        {
            q.push(i - j);
            j = next[j];	//把这个位置标为不匹配 继续找直到i = s1.lenght()
        }
    }
    while(!q.empty())
    {
        cout << q.front() << endl;
        q.pop();
    }
}

全部代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<iostream>
#include<string>
#include<queue>
#include<cstdlib>
using namespace std;

int* getNext(string s2)
{
    int* next = (int*)calloc(s2.length(),sizeof(int));
    next[0] = -1;
    int k = -1;
    int j = 0;
    while(j < s2.length())
    {
        if (k == -1 || s2[j] == s2[k])
        {
            next[++j] = ++k;
        }
        else
        {
            k = next[k];
        }
    }
    return next;
}

void KMP(string s1,string s2)
{
    int i = 0,j = 0;
    queue<int> q;
    int* next = getNext(s2);
    while(i < s1.length())
    {
        if(j == -1 || s1[i] == s2[j])
        {
            i++;
            j++;
        }
        else
        {
            j = next[j];
        }

        if(j == s2.length())
        {
            q.push(i - j);
            j = next[j];
        }
    }
    while(!q.empty())
    {
        cout << q.front()+1 << endl;
        q.pop();
    }

    for (int i = 1; i <= s2.length();i++)
    {
        cout << next[i];
        if(i!= s2.length())
            cout << " ";
    }
}

int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    KMP(s1, s2);
    return 0;
}

同时也是luogu模板题的代码。

参考链接

  1. 1. KMP算法 —— 字符串匹配
    1. 1.1. 一般写法
    2. 1.2. 第一次优化 普通KMP（无next计算优化）
    3. 1.3. 第二次优化 next计算的优化
    4. 1.4. 代码们
    5. 1.5. 参考链接